統計学と金融工学についての習得が必要そうだというのが見えてきた。
リターンの理解は簡単だろう。
一定期間のうちで投資対象がどれだけ価額が増えるかということだ。
一方でリスクとは何だろうか。
これは平均リターンからのばらつき、と表現される。
統計学の用語で言えば標準偏差という。
このように聞くとリターンのほうが簡潔で、
リスクのほうが計算が難解に思える。
だがしかし、神様に組み込むアルゴリズムとして、
本当にそんな単純でいいのだろうか。
むしろリスクの方が信頼できる値を計算でき、
リターンの計算のほうが難しいと思っている。
過去10年のリターンを計算するとなれば、
10年前の価額と現在の価額を比較することになる。
過去30年のリターンを計算するとなれば、
30年前の価額と現在の価額を比較することになる。
いずれも現在の時間軸が比較の基準となる。
それは少々おかしいのではないだろうか。
たまたま現在の相場が良ければ、
過去何年間分のリターンであっても良く見えるし、
たまたま現在の相場が悪ければ、
過去何年分のリターンであっても悪く見える。
いま現在の価額が良いか悪いかはあるにしても、
あくまでリスクに加味されるばらつきの要素でしかなくて、
リターンの値の算出基準とするべきではないのではないだろうか。
単純なリターンの算出方法では、
現在の価額の数値が持つウェイトが大きすぎる。
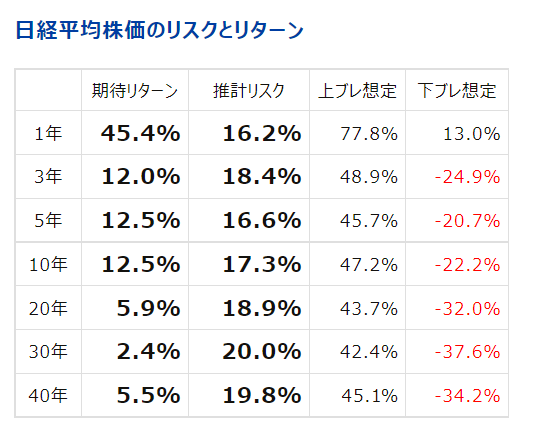
上の表を見れば分かるように、
リターンの値はぶれが大きすぎて参考にできない一方で、
リスクの値は16~20%での推移で概ね安定している。
リターンを算出するのに何かいい方法はないかと検討していると、
下記のような記述を見つけた。
各資産クラスの中長期的な期待リターンを算出するには、世界各国の人口動態や生産性、技術革新、景気サイクル、金融政策の見通しなど、非常に多岐にわたる要因を考慮しなければなりません。
資産運用における「期待リターン」の考え方・求め方 | 富裕層向け資産防衛メディア | 幻冬舎ゴールドオンライン
これは唐突に、なんとも気の遠くなる規模の話になってきた。
やはり単純なリターン率など、いくら求めても無意味だったのである。
さて、そうなれば餅は餅屋だ。
素直に「長期マーケット予測(Long-term Capital Market Assumptions:LTCMAs)」とやらを
参考にさせてもらおう。
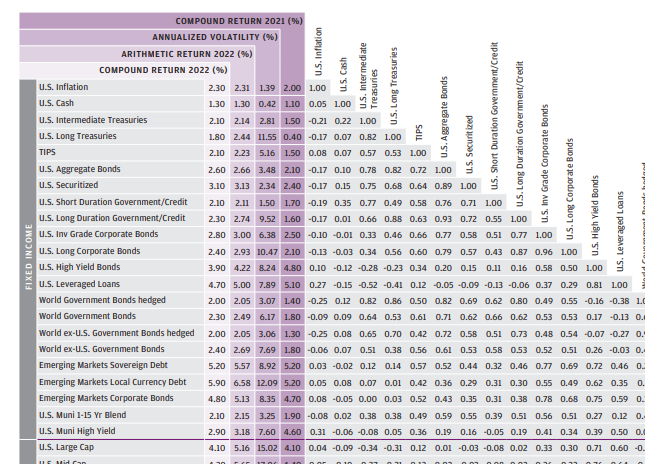
あぁ、なんとも素敵ではないか。
算術平均リターンに、幾何平均リターン、年率換算偏差、それに相関係数まで載っている。
しかし、究極的には個別株についてもこれを算出したい。
この計算式を確立するには本当に長い道のりになるだろうが、
ひとまずはこの値をベースとして、色々なアルゴリズムに応用してみよう。